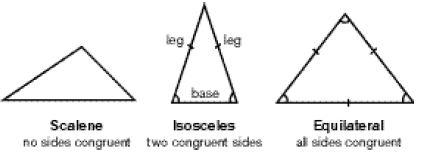
Rene Descartes was a very important and famous philosopher of the 17th century. He mostly focused on life in general, but was indeed very important to modern-day mathematics, especially geometry.
In 1637 he published his world changing book called "Discourse on Method". This book was extremely important to algebra (and of course geometry, since algebra and geometry are majorly related) because he began using standard lowercase notations such as: a, b, c for known quantities and x, y, z for unknown quantities. This was an incredible "invention" for even today, almost 380 years later, we still use it in everyday geometry and overall math.
Later he also stated that each point in a 2D plane, can be described as two numbers; one showing horizontal location and the other one describing vertical location. He used perpendicular lines to discover the point's x (horizontal) and y (vertical) coordinates. This can be seen on the figure below:

He was also able to create "a rule of signs" technique which many stated to be his most important contribution to geometry as we know it. This technique determined the number of positive and/or negative (real) roots of a polynomial. He also popularised the notion of exponents throughout major parts of Europe.

He was an incredible philosopher, a great physician, but most importantly; he was an outstanding mathematician which shaped math itself. Some may even consider him one of the funding fathers of geometry!
In 1637 he published his world changing book called "Discourse on Method". This book was extremely important to algebra (and of course geometry, since algebra and geometry are majorly related) because he began using standard lowercase notations such as: a, b, c for known quantities and x, y, z for unknown quantities. This was an incredible "invention" for even today, almost 380 years later, we still use it in everyday geometry and overall math.
Later he also stated that each point in a 2D plane, can be described as two numbers; one showing horizontal location and the other one describing vertical location. He used perpendicular lines to discover the point's x (horizontal) and y (vertical) coordinates. This can be seen on the figure below:

He was also able to create "a rule of signs" technique which many stated to be his most important contribution to geometry as we know it. This technique determined the number of positive and/or negative (real) roots of a polynomial. He also popularised the notion of exponents throughout major parts of Europe.

He was an incredible philosopher, a great physician, but most importantly; he was an outstanding mathematician which shaped math itself. Some may even consider him one of the funding fathers of geometry!

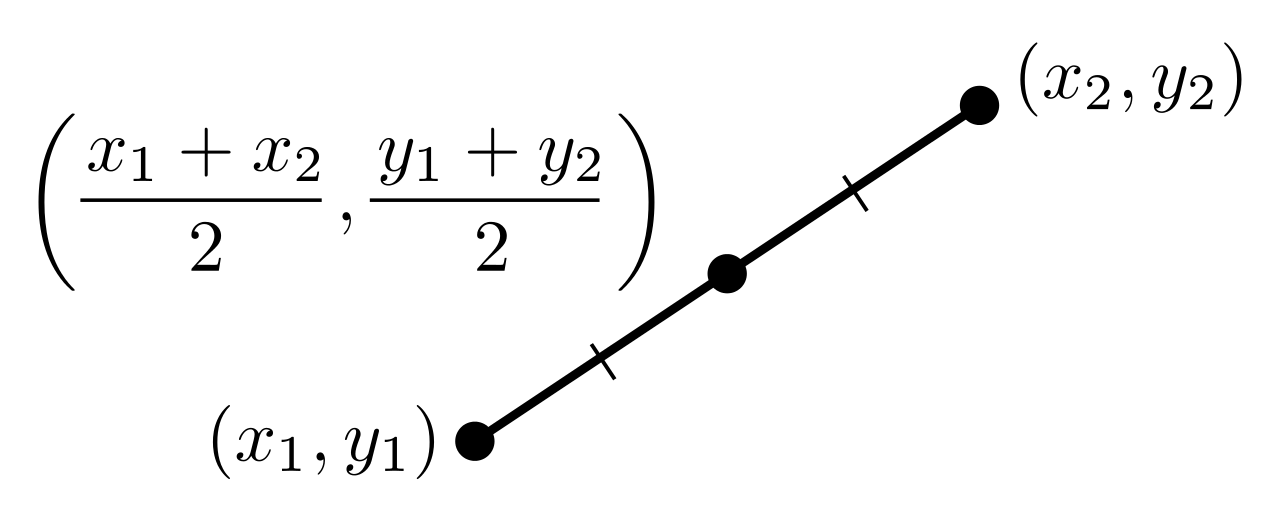
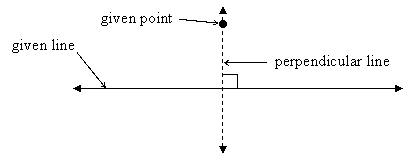









 through point Y. Call this line
through point Y. Call this line 
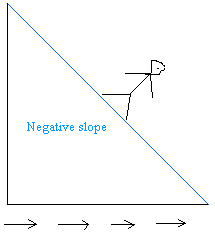
 1 + m
1 + m